Trigonometry
Created | Updated Jun 14, 2007
Trigonometry is the branch of mathematics that concerns itself with the measurement of triangles. Mathematicians have been enamoured of triangles for thousands of years to the point where entire textbooks and classes are devoted to their measurement.
Despite the mathematical tomes dedicated to triangle measurement, there are only a few key things you really need to know in order to have a functional grasp of trigonometry.
Some Basics
The three angles in a triangle add up to 180°.
One of the angles in a right-angled triangle1 is equal to 90°.
The hypotenuse of a right-angled triangle is the side opposite the 90° angle. It is also the longest side of a right-angled triangle.
Pythagoras' Theorem
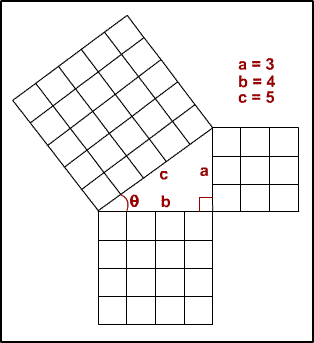
Pythagoras was an ancient Greek philosopher-mathematician who lived around 500 BC. Among his claims to fame is the abstraction of mathematics2. His best known achievement, though, was to borrow a theorem that had been well-known among the Babylonians for 1,000 years, and name it after himself.
This theorem states the relationship in a right-angled triangle between the hypotenuse and the other two sides.
Pythagoras' Theorem states:
c2 = a2 + b2
Where c is the length of the hypotenuse, and a and b are the lengths of the other two sides.
You can see this in Diagram One, where Pythagoras' Theorem shows that:
52 = 42 + 32
Thanks to some Babylonian ingenuity and Pythagoras' promotion, you can calculate the length of any side of a right-angled triangle, provided you already know the length of the other two sides. For example, if we only knew the lengths of the two shortest sides in the triangle in Diagram One, then we could use Pythagoras' Theorem to come up with:
c2 = 42 + 32
c2 = 16 + 9 = 25
To give c = 5.
SOHCAHTOA

About the same time Pythagoras was busy finding out the length of the sides of a right-angled triangle, the Mayans were upgrading the Mayan calendar and needed tools to describe the angles of triangles. From their work we derive trigonometric functions, the most important of which are sine, cosine, and tangent.
The Mayans realised that various properties of the angles of right triangles could be expressed as ratios between the sides of the triangles.
The Mayans also determined that for one of the non-right angles in a right-angled triangle, which we'll call θ3, these properties4 hold:
The sine of θ is equal to the length of the side opposite the angle, divided by the length of the hypotenuse.
The cosine of θ is equal to the length of the side adjacent to the angle, divided by the length of the hypotenuse.
The tangent of θ is equal to the length of the side opposite the angle, divided by the length of the side adjacent to the angle.
Or, to state things more succinctly, referring to Diagram Two:
Sin θ = Opposite/Hypotenuse
Cos θ = Adjacent/Hypotenuse
Tan θ = Opposite/Adjacent
A perfect mnemonic device for remembering these relationships is SOHCAHTOA.
| SOH | CAH | TOA |
|---|---|---|
| Sin θ = Opp/Hyp | Cos θ = Adj/Hyp | Tan θ = Opp/Adj |
SOHCAHTOA gives us the ability to determine the value of any angle in a right-angled triangle, given the lengths of any two of the sides.
For example, let's consider the angle created where the hypotenuse c meets side b in Diagram One above, and let's pretend we only know the lengths of a and b (though a similar process could be done with any two sides and a different trigonometric function). We can find the value of this angle using any pocket calculator with trigonometric functions, as follows.
First, we only have the lengths of the opposite (a) and adjacent (b) sides, so let's look at SOHCAHTOA to see which of the three equations we can use. It's the TOA part, and we get:
Tan θ = Opp/Adj = 3/4 = 0.75
To convert from the tangent of the angle to the angle itself, you need the 'inverse' tangent, which is normally shown on calculators as tan-1. Try it out and you'll find that the value of the angle in Diagram One is 36.87° (or 0.644 radians, if you're into that sort of thing).
The Unit Circle
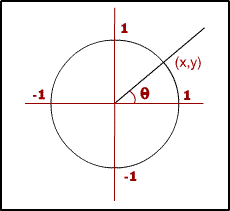
The unit circle is simply a circle whose centre is on the Cartesian origin (0,0), and whose radius is 1.
The most interesting thing about the unit circle, as far as trigonometry is concerned, is that it gives us the values of sine and cosine5 for any angle.
In Diagram Three we're measuring the angle θ between the x-axis of the Cartesian plane and a line that extends from the origin. Now, here's the really interesting thing; the sine of the angle is equal to the y-coordinate of the point on the unit circle where the line crosses, and the cosine of the angle is equal to the x-coordinate. This is true for any line extending from the origin.
Why is this? Well, the line segment from the origin to the point where it crosses the unit circle forms the hypotenuse of a right-angled triangle. Because the radius of the circle is 1, the length of the hypotenuse is likewise 1. SOHCAHTOA's rules then boil down to:
Sin θ = Opposite
Cos θ = Adjacent
Tan θ = Opposite/Adjacent
In other words:
Sin θ = y
Cos θ = x
Tan θ = y/x

