Packing Algorithms
Created | Updated Oct 19, 2009
In many everyday situations, we have to pack objects into a given space. Normally, this isn't much of a problem - either there are very few objects to be packed, or there is a large amount of space. However, in some circumstances, we need to be as efficient as possible. How many times have you had to unpack and repack the car boot, just to be able to go on holiday for a week?
Bin Packing
In this entry, we will look at algorithms that could be used to pack bins1. In this situation, we have a number of bins, all of the same size, and our blocks, which may be of any size. To simplify matters, we will assume that the width and depth of the all blocks is the same - and will fit snugly into our bins. Thus we are left with a one-dimensional problem.
Suppose our bins are 150cm high and our blocks are of the following heights:
| Block: | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height (in cm): | 80 | 70 | 40 | 90 | 60 | 90 | 50 | 50 | 60 | 70 | 80 |
How Should We Pack Them?
We will examine three heuristic algorithms and look at the differences between the results. Heuristic algorithms attempt to find a 'reasonable' result in a 'reasonable' amount of time. They may not necessarily find the best possible result, however, the amount of time saved by finding a non-optimal solution usually compensates for the losses caused when compared with a perfect solution.
The Full Bin Algorithm
In this algorithm, we look for combinations of blocks that will completely fill a bin. If we find such a combination, we put it into a bin and move to the next bin. Any remaining blocks (which cannot be used to completely fill a bin) we put in the next available bin. If there are more blocks than will fit in one bin, we choose a combination of blocks that will make the first available bin as full as possible.
So in our example, blocks A & B, D & E, F & I, J & K all form combinations of 150cm. The remaining blocks, C, G & H, have a combined height of 140cm, so we put all of these in the next bin. Thus we could pack all the blocks into five bins.
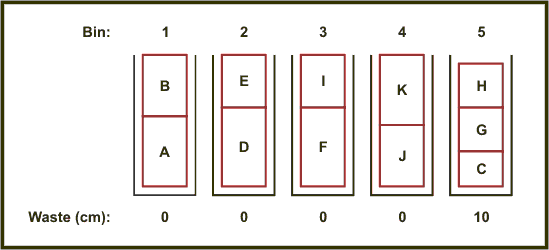
Under each column you will notice a number - this is an indication of how much space is being wasted in each bin. This will allow us to see how efficient our algorithm is. The first four bins have no waste at all, because the bins are completely full. The fifth bin has a waste of 10cm, because the blocks have a combined height of 140cm. However, we should not pay too much attention to this - there is no way we could have completely filled this bin, as we had run out of blocks.
Before we put any blocks into bins, we had to make a lot of comparisons to find combinations of blocks that would completely fill a bin. In situations where we have a large amount of data, this would invariably take up a lot of time, possibly longer than is acceptable. The algorithm will run fairly quickly in our example, as we have only 11 blocks.
The First-Fit Algorithm
In this algorithm, we simply put each block into the first bin with enough free space. So, block A goes into the first bin, followed by block B. There is no more room in this bin, so blocks C & D go into bin 2. There is still 20cm spare, but block E is too big, so goes into bin 3, along with block F. Blocks G & H are put into bin 4, leaving 50cm free. But none of the remaining blocks are small enough to go in there! So I & J go into bin 5, and K is on its own in bin 6.
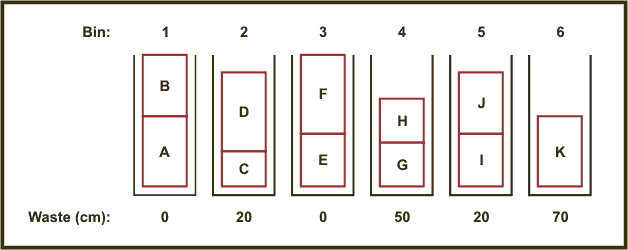
This algorithm is clearly not as efficient for our example - we needed six bins and wasted a whopping 160cm. However, we did only need to look at each block once - and find the first bin it would fit in.
You might be thinking 'Isn't there some way we can improve this algorithm?' Well, yes there is.
The First-Fit Decreasing Algorithm
This time, we put the blocks into decreasing size order first (possibly by using a sorting algorithm). In our example, the order becomes:
| Block: | D | F | A | K | B | J | E | I | G | H | C |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Height (in cm): | 90 | 80 | 70 | 60 | 50 | 40 | |||||
Having done this, we use the first-fit algorithm, putting each block into the first bin with enough free space. So, D goes into the first bin. F won't fit in there, so goes into the second bin. A is put into bin 3, and K into bin 4. Block B will now fit in bin 3, above block A. Similarly block J goes in bin 4. Blocks E & I go into bins 1 and 2 respectively, which leaves G, H & C to go into bin 5.
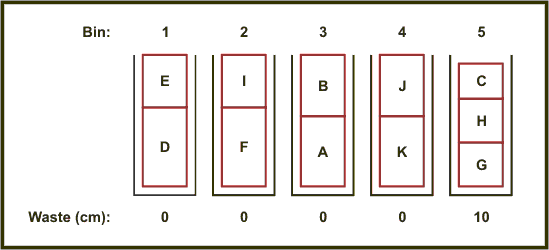
This algorithm is as efficient as the 'full bin' method in terms of wasted space - there is only 10cm of empty space left.
A Final Word
The first-fit algorithm is an example of a 'greedy' algorithm. It gets this name because at each step a decision is made based entirely on the current situation of the bins - regardless of what other blocks there are to be packed. It 'gobbles up' the best resources.
In this entry we have only measured the efficiency of our algorithms by how much space was wasted. We have noted (in passing) that the full bin algorithm takes a lot of time finding combinations of blocks to fill the bins - if we were to do a proper analysis, we would examine the number of operations required for each algorithm. We would also use the 'big O' notation, to compare the complexity of each algorithm.

