Size Matters: How big are molecules?
Created | Updated Jan 9, 2012
Molecules are the building blocks of the stuff we use in our everyday lives. They are made of atoms which are bound together. The understanding and the design of molecules is traditionally a part of chemistry. Apart from their incomprehensibly bizarre chemical behaviour, which will not be discussed in this Entry, one of the important characteristics of molecules is their size. Some examples: Many drugs work by jamming reactive positions in other bigger reacting molecules (aka enzymes). This is a clear size effect - it's like jamming a lock by inserting a key that is just too big to fit. Many industrial catalysts can be designed on a molecular level, so that the molecules interacting with them will have to bump into bulkier parts - in that way the catalyst passively steers the reactants into certain desired orientations. Another example: Some porous materials have pores so tiny, that they can be used to 'sieve' molecules according to their size; these materials are therefore called 'molecular sieves'; sometimes they are also called zeolites1. Molecules can also be designed to fit these pores and to seal them shut (one will have to know the size of the pore and of the molecules). Many applications can be thought of just by considering the movement of molecules in structured environments. Much of the 'nanotechnology' and the concepts of nano-robots and intelligent materials will have to deal with the effects of molecular sizes and shapes.
The size and shape of molecules
Many may already have seen structural formulas in chemistry schoolbooks (if not, some can be found in the steroid hormones Entry). Those formulas resemble the actual shape of the molecules. It is not possible though to measure the length of a molecule by measuring the length of the formula with a ruler and scaling it down. However, since most bond lengths (the distance between the centres of two connected atoms) and Van der Waal's radii (which will be explained later) are known, one can reconstruct the lengths with some basic trigonometry and a pocket calculator.
Bond lengths
The length of most bonds, or the distance between two bound atomic nuclei, are known from X-ray crystallographic data2. Their length is typically in the order of one or two hundred picometres3. The bond length varies with the number of bonds between two atoms. That is, triple bonds will be shorter than double bonds which in their turn are shorter than single bonds. They also vary with the types of atoms that are bound together. For example, if there is additional electrostatic attraction between the atoms, the bond length will be shorter.
For convenience, some of the most common bond lengths are given in the following list (the elements are abbreviated according to the The Periodic Table of the Elements4):
Selected bond lengths- C-H (single): 109 pm
- C-C (single): 154 pm
- C=C (double): 134 pm
- C≡C (triple): 120 pm
- C-O (single): 142 pm
- C=O (double): 122 pm
- C≡O (triple): 107 pm
- C-N (single): 147 pm
- C=N (double): 122 pm
- C≡N (triple): 111 pm
- C-F (single): 136 pm
- C-Cl (single): 176 pm
- C-Br (single): 191 pm
- C-S (single): 181 pm
- O-H (single): 96 pm
- N-H (single): 101 pm
- N-O (single): 145 pm
- N=O (double): 117 pm
- Benzene hexagon width from point to point: 280 pm
Van der Waal's radii
Measuring the length of the bonds is not enough to determine the effective length of a molecule. This length is equivalent to the distance between atomic nuclei. However, the nuclei are surrounded by electrons, which will act as a sort of bumper, by repelling the electron-bumpers from other molecules that come close. To obtain the effective length of a molecule one must therefore also add the corresponding Van der Waal's radius, which is the effective radius of those bumpers, to both ends of the line. The bumpers are not strictly rigid like snooker balls; they have some flexibility, like balloons. For this reason the length obtained is generally the upper length limit for those molecules, they can however be shorter by some ten or 50 pm. In some cases, for example if they are compressed in a solid material, the entire molecular geometry can deform; in that case the molecule can become significantly shorter.
Selected Van der Waal's radii- H:120 pm
- CH3:200 pm
- N: 155 pm
- O: 152 pm
- S: 180 pm
- F: 147 pm
- Cl: 175 pm
- Br: 185 pm
Bond Angles
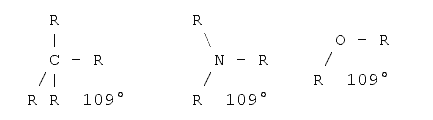
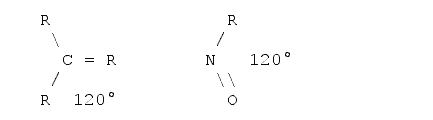
To measure the length of a molecule one should also be aware of the fact that molecules are three-dimensional objects. That is, what one is able to see on a sheet of paper or on the screen is a projection onto a two-dimensional plane. In a first approximation it is quite easy to determine the projections if one knows the basic angles between the bonds. There are basically three standard angles for organic compounds one should know. The tetrahedron angle of 109° when all the bonds from this atom to all the other atoms are single bonds (i.e. just one dash). The hexagon angle 120°, when one atom has one double bond to another atom, and the line angle of 180° when an atom has either two double bonds or one triple bond to another atom. The real angles often differ from those angles as some other effects must be taken into account - for example the valence shell electron pair repulsion5,6, electrostatic interactions between the substituents and ring tension. However, for a first estimation these angles can be used. Examples follow:
Tetrahedral angle
Planar angle (hexagon angle)
Axial angle (triple bonds or two double bonds7)
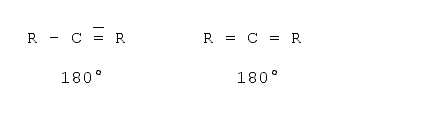
Two Examples
In the following two examples the length will be determined by looking up the table and by doing some primitive trigonometric calculations. The two example molecules are TNT, which is used in mining and by demolition companies, and a Perrylene derivative, which is used as a fluorescent dye.
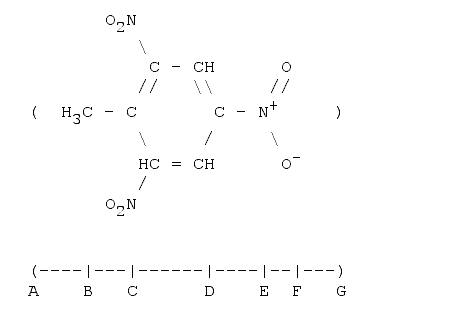
1. 2,4,6-trinitro-toluene (TNT)
2. N-methyl-perrylene-diimide
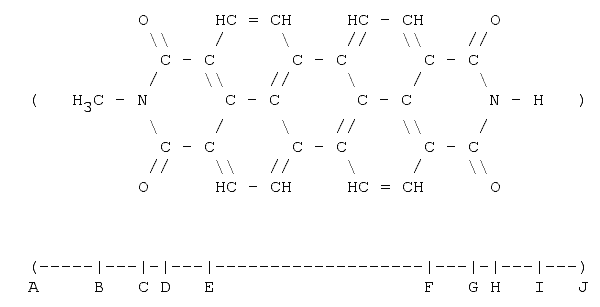
Toluene: A-B is the Van der Waal's radius of CH3, B-C the bond length (single) between two carbon atoms, C-D the width of a benzene ring, D-E the bond length (single) between a carbon and a nitrogen atom. So far we have 781 pm. The next length E-F is given by the projection of the mean N-O bonds onto the measured line. The mean length is 131 pm and the projected length (the angle N-O-Plane is 60°) is cos(60°)·131, or 66 pm. F-G is the van-der-Waals radius of Oxygen. The total length is then: 999 pm, or almost 1 nm.
N-methyl-perrylene-diimide: By looking at the formula one would assume that this molecule is roughly two times longer than TNT. A-B is the Van der Waal's radius of the methyl (CH3) group, B-C the bond length (single) between carbon and nitrogen. C-D is the projection (60°) of a single carbon-nitrogen bond. D-E is the length of a single carbon-carbon bond. So far we have: 575 pm. E-F is equivalent to two and-a-half benzene-hexagons in length (pure geometry - in case of doubt the author recommends drawing the five hexagons between E and F and checking out); that is 700 pm. So, The length of the segment A-F is 1275 pm. G-H is the same as B-c (74 pm) and H-I is the bond length between a nitrogen and a hydrogen atom. I-J is the hydrogen Van der Waal's radius. The total length is then 1570 pm or 1.6 nm.
The Length and Shape of Molecules - More Details
The method described above yields a quite good approximation for the length of a molecule along an arbitrary line. The geometry can eventually become a lot more three-dimensional for more complicated molecules, but the principle is the same - looking up tables, calculating projection lengths and adding Van der Waal's radii to the ends. Meanwhile, computers are good enough to calculate quite complicated molecules from scratch. They do it by optimising the electrostatic distances between the atoms and doing some quantum mechanical calculations for the bond geometry. The advantage of these calculations is that they are quite precise, and that they allow to predict some further properties, like the spectral behaviour and whatnot. The disadvantages are that the calculations often disregard the environment that affects the molecule - for example, the distortions caused by locking the molecule up in a water-filled molecular sieve. To account for that, even bigger computers need to be built. In many cases the experienced chemist will have a feeling about where distortions might happen and how short molecules can get - this intuition often surpasses computer-resolved structures.
To confirm if the obtained data is correct, the ultimative precise method is to go and measure the molecules. This can be done by analysing X-ray diffraction patterns or by recording more-dimensional nuclear magnetic resonance (NMR) spectra8 - for example. However, these techniques cannot be used to measure everything. The X-ray diffraction technique needs well-organised crystals; it is very difficult to gain information from liquids using this technique. The appreciation of nuclear magnetic resonance spectra and the interpretation thereof is an art in itself, very time-consuming and tremendously difficult to perform for complicated molecules, even with the aid of supercomputers.
In conclusion, it is often helpful to estimate the size of a molecule by looking at the rough angles and bond lengths. There are more accurate methods, but these are very time-consuming and often require a firm background in maths and quantum mechanics. The ultimative accurate values for the size and shape of a molecule would be obtained by measuring the molecule. The available methods, however, are quite limited and expensive.

